Борис Манзон
Появившаяся в начале 60-х годов и быстро увеличивающая свою мощность компьютерная техника позволяет решать многие научные и инженерные задачи, которые не поддавались аналитическим методам. К середине 70-х годов были накоплены целые библиотеки алгоритмов численного решения таких задач. К числу лучших из них следует отнести библиотеки матричных алгоритмов LINPACK и EISPACK Департамента энергетики США. Они представляют собой собрание тщательно проверенных и оптимизированных алгоритмов, разрабатывавшихся в течение многих лет ведущими мировыми специалистами. Но с их появлением появилась необходимость в обеспечении кратчайшего доступа широкой аудитории инженерных и научных работников к этому изобилию алгоритмов. Собственно говоря, создание языка Matlab (сокращенно от Matrix Laboratory - “матричная лаборатория”) и было обусловлено этой необходимостью.
Когда в 1978 г. Клив Моулер (Cleve Moler), разработчик системы Matlab, предложил в качестве основного объекта языка Matlab использовать двухмерный массив (матрицу), не требующий задания размерности, наверное, он и не предполагал, насколько эффективным окажется новый язык для написания матричных алгоритмов.
Matlab за прошедшие годы приобрел большую популярность, постепенно переместившись с больших вычислительных систем на персональные компьютеры, сама же программа вместе со всеми профессиональными приложениями превратилась в мощную систему, охватившую широкий спектр научных, инженерных и экономических приложений.
В данной статье мы опишем возможности последней версии программы - Matlab 5.х, - которая по своим функциональным характеристикам значительно превосходит предыдущую версию - Matlab 4.х.
Комплект поставки
Matlab 5.х компании MathWorks включает CD-ROM с установочными файлами программ Matlab, Simulink и 20 дополнительными профессиональными приложениями (Toolboxes). Каждая из упомянутых программ устанавливается самостоятельно только в случае приобретения лицензии на нее. На диске находится также полная электронная документация на указанные программы в форматах HTML и Adobe Acrobat (PDF).
Помимо CD-ROM в комплект поставки входит бумажная документация: учебник для начинающих (Getting Started with Matlab); руководство для разработки графического интерфейса (Building GUIs with Matlab); руководство по установке и использованию Matlab Notebook - документа Matlab, использующего в качестве редактора текстовый процессор Microsoft Word; руководство по обеспечению взаимодействия с внешними программами, такими, как Си, Фортран, и коммуникационными программами (Appliccation Program Interface Guide); руководство по новым функциям пакета и обеспечению совместимости со старыми версиями (Matlab 5 - New Features); два объемных руководства по использованию Matlab (Using Matlab и Using Matlab Graphics). Приобретя лицензию на Simulink и профессиональные приложения, вы дополнительно получаете и документацию по этим продуктам.
Платформы
Matlab 5.х может работать на компьютерах IBM PC под управлением Windows 3.1 (с дополнительно установленной подсистемой win32s), Windows 95 и Windows NT, на компьютерах Macintosh и более мощных машинах под управлением UNIX. Читателям этой статьи предлагается описание Windows-версии программы.
Требования к аппаратному и программному обеспечению
Версия под Windows 95 занимает на жестком диске от 25 до 115 Мб в зависимости от размера кластеров и количества устанавливаемых файлов помощи; необходимая оперативная память - 8 Мб, рекомендуется 16 Мб. Желательны графический акселератор, звуковая плата, компиляторы Си и Фортрана.
Для работы Matlab Notebook необходим текстовый редактор Microsoft Word версий 6.0 или 7.0 либо Microsoft Office 97. Для просмотра файлов помощи можно использовать Internet-браузер (Microsoft Internet Explorer 3.0, Netscape Navigator 3.0) либо просмотрщик PDF-файлов (Adobe Acrobat).
Отличие Matlab от других программ автоматизации математических расчетов
Подобно языкам высокого уровня, приспособленным для разработки программ численного моделирования, таким, как Си или Фортран, Matlab имеет эффективные средства для процедурного, объектно-ориентированного и визуального программирования, мощные средства отладки программ и разработки пользовательского интерфейса. Все это дает основание считать Matlab высокопроизводительным языком технического программирования. Однако есть и существенные отличия:
- основным элементом, которым оперирует Matlab, является не число, а двухмерный массив - матрица, это позволяет многие технические вычислительные задачи, особенно в матричной и векторной формулировках, решать гораздо быстрее, чем при написании программ на скалярном неинтерактивном языке, какими являются Си или Фортран;
- Matlab - интерактивная система, язык Matlab - это язык команд, представляющих собой готовые алгоритмы тех или иных вычислений (например, одной командой можно решить систему линейных уравнений или построить график сложной функции);
- язык Matlab специально предназначен для решения научно-технических задач, численного моделирования систем и процессов.
Обладая возможностями графической визуализации, сопоставимыми со средствами универсальных пакетов для автоматизации математических расчетов, таких, как Mathematica или Maple, Matlab существенно отличается и от них:
- при том, что язык Matlab не приспособлен для создания программ символьных вычислений, он более удобен и эффективен при написании программ численного моделирования (один из пакетов Matlab содержит символьный модуль Maple, правда, он не столь эффективен, как программа Maple, и не позволяет создавать символьные программы);
- программа Matlab не имеет “способностей” представления формул с высоким полиграфическим качеством, что необходимо для оформления научно-технической публикации (поставляемый с последней версией программы модуль Matlab Notebook, интегрирующий Matlab с текстовым процессором Microsoft Word, несколько сглаживает этот недостаток). В то же время, в отличие от упомянутых универсальных математических пакетов, она имеет развитые средства для создания графических интерфейсов к программам технического моделирования.
И все-таки основное преимущество Matlab перед упомянутыми программами состоит в том, что в ней в самосогласованной, удобной для использования форме интегрировано большое количество мощных, эффективных алгоритмов. Воистину эту систему можно назвать симфонией алгоритмов.
Математика и вычисления в среде Matlab
Программа Matlab не так удобна для проведения математических расчетов в интерактивном режиме, как, например, Mathematica или Maple V, поскольку не позволяет редактировать введенные команды и располагать на рабочем документе текст и графики. Однако она дает возможность записывать последовательность команд и их результаты. Для этого с помощью команды diary <имя файла> нужно открыть файл записи. Закрыть его (закончить запись) можно, используя команду diary off.
Линейная алгебра
Как уже упоминалось, Matlab - пакет матричной математики. Основным объектом, с которым он оперирует, является матрица, не требующая задания размерности; любое имя или число, введенное в командную строку, также по умолчанию предполагается матрицей. Именно поэтому математика линейной алгебры - наиболее мощная часть программы. Matlab умеет производить все необходимые операции с матрицами: складывать, умножать, обращать матрицы и находить их определители, находить собственные векторы и значения, матричные экспоненты и логарифмы, вычислять корни из матриц, решать системы линейных уравнений и т. д.
Запись многих операций с матрицами соответствует общепринятой нотации аналогичных численных операций. Поэлементное сложение и вычитание массивов записывается так же, как сложение и вычитание чисел; умножение матриц обозначается символом *, для поэлементного умножения и деления матриц используются соответственно знаки .* и ./. Деление матрицы A на матрицу B обозначается как A/B (правое деление - решение уравнения x*A=B) либо AB (левое деление - решение уравнения A*x=B).
В программе имеются команды для создания случайных и известных стандартных матриц. Например, командами
[A=rand(4,4), V=rand(4,1)]
[A =
0.9501 0.8913 0.8214 0.9218
0.2311 0.7621 0.4447 0.7382
0.6068 0.4565 0.6154 0.1763
0.4860 0.0185 0.7919 0.4057]
[V =
0.9355
0.9169
0.4103
0.8936]
создаются случайные матрица A размерностью 3х3 и вектор V размерностью 3.
Командой
[X=AV]
[X =
-0.8224
0.0123
1.2599
0.7278]
находится решение системы линейных уравнений A*X=V.
В версию Matlab 5.0 добавлены новые алгоритмы для операций с матрицами: команда cholinc неполной факторизации Чолеску; команда gallery, вызывающая более 50 различных тестовых матриц; команда luinc неполной LU-факторизации; команда repmat для многократного дублирования и мозаичного размещения массива и, наконец, команда sprand для создания случайных однородно распределенных разреженных матриц.
Например:
[gallery(‘krylov’,A)]
[ans =
1.0000 3.5846 8.4382 19.5100
1.0000 2.1761 4.5684 10.3922
1.0000 1.8550 4.6103 10.7382
1.0000 1.7021 3.9420 9.4357]
Полиномы
Достаточно широким набором функций оперирует математика полиномов. Полиномы в Matlab представляются вектором коэффициентов. Так, введенный нами случайный вектор V соответствует полиному третьей степени с коэффициентами:
[P=V’]
[P =
0.9355 0.9169 0.4103 0.8936]
Программа позволяет находить все корни полиномов, вычислять характеристические полиномы матриц, перемножать и делить полиномы, находить подгоночную полиномиальную функцию, связывающую два набора данных, выполнять полиномиальную интерполяцию функций.
Например, командой
roots(P)
ans =
-1.2445
0.1322 + 0.8661i
0.1322 - 0.8661i
можно найти корни определенного выше полинома.
Пятая версия дополнена новыми функциями многомерной интерполяции: interp3 - трехмерная интерполяция данных; interpn - многомерная интерполяция (обращение к таблице); ndgrid - создание массивов для многомерных функций и интерполяции.
Следующая команда производит четырехкратную кубическую интерполяцию данных, заданных матрицей A, командой mesh строится полученная интерполирующая поверхность (рис.1):
zi=interp2(A,4,’cubic’);
mesh(zi)
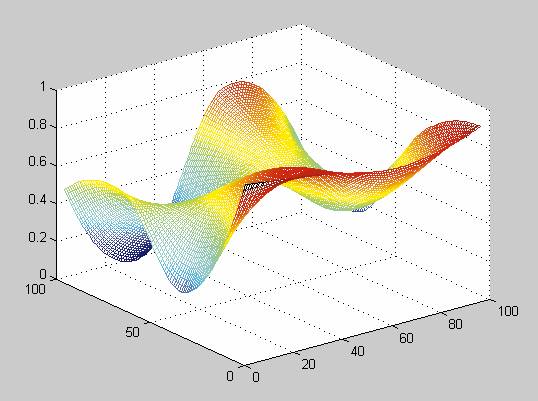
Рис. 1. Поверхность, интерполирующая данные, заданные в виде матрицы
Функции
Matlab содержит более 500 математических, статистических и других функций научно-технического назначения.
Библиотека математических функций Matlab представляет собой обширное собрание вычислительных алгоритмов - от элементарных функций (таких, как сумма, синус, косинус) и комплексной арифметики до сложных операций с матрицами, специальных функций (скажем, функций Бесселя), быстрого преобразования Фурье и т. д.
Функции в Matlab вводятся в знакомой математической нотации, причем в применении к массиву они действуют на каждый его элемент - например, так строится график поверхности z=sin(x*y).
Сначала командой
[x,y]=meshgrid(-3:0.1:3,-3:0.1:3);
создаются вспомогательные массивы x и y, необходимые для построения графика (координатная сетка). Затем командой
[z=sin(x.*y);]
находятся значения функции в точках координатной сетки и, наконец, командой
[surfl(z)]
строится график поверхности z=sin(x*y) (рис. 2).

Рис. 2. График поверхности z=sin (x*y)
В версию 5.0 программы вошли новые элементарные и специальные функции: airy - функции Эйри; besselh - функции Бесселя третьего рода (функции Ханкеля); dblquad - численное двойное интегрирование; mod - вычисление по модулю; normest - оценка нормы матрицы; новые функции для операций с датами и временем: calendar, datenum, datestr, datetick, datevec, eomday, now, weekday и некоторые другие.
Обыкновенные дифференциальные уравнения
Matlab предлагает самые современные алгоритмы численного решения обыкновенных дифференциальных уравнений, в том числе жестких; имеются также команды для построения графиков решения дифференциальных уравнений и фазовых траекторий.
В последнюю версию программы включены новые численные методы: ode45, ode23, ode113, ode23s, ode15s, а также команды: odefile - для постановки задач решения обыкновенных дифференциальных уравнений; odeset - для создания и редактирования входных аргументов команд решения обыкновенных дифференциальных уравнений; odeget - для извлечения опций входных аргументов, созданных командой odeset.
В качестве примера покажем, как Matlab решает известную систему обыкновенных дифференциальных уравнений Лоренца. Вначале запишем m-файл для вычисления правых частей системы (рис. 3) и запомним его под именем lorenz.

Рис. 3. m-файл для решения системы обыкновенных дифференциальных уравнений Лоренца
Введем вектор начальных значений
[x0=[-0.7 -0.7 1];] и временной диапазон
[t0=0;]
[tf=100;]
Теперь можно вызвать команду решения дифференциальных уравнений (используем метод Рунге - Кутта 4 - 5-го порядка):
[[t,x]=ode45(‘lorenz’,[t0,tf]’,x0’);]
Можно нарисовать траекторию движения точки (решение) в трехмерном пространстве с помощью следующей команды (рис. 4):
[comet3(x(:,1), x(:,2), x(:,3))]

Рис. 4. Тректория движения точки (решение) в трехмерном пространстве
Математика разреженных матриц
В разреженных матрицах ненулевых элементов гораздо меньше, чем нулевых. Такие матрицы возникают при решении многих задач, например при интегрировании уравнений в частных производных, в задачах распознавания образов, в теории графов и многих других. Matlab оперирует разреженными матрицами больших размеров, пользуясь эффективными функциями их формирования, преобразования, разложения и вычисления.
В качестве примера на рис. 5 показано, как с помощью команды SPY на дисплей выводится изображение ненулевых элементов симметричной разреженной матрицы.
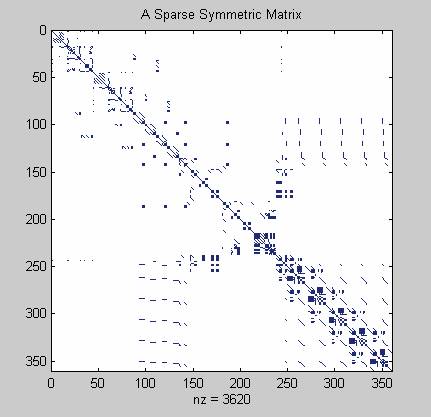
Рис. 5. Ненулевые элементы разреженной матрицы
В версию Matlab 5.x добавлены команды: bicg - метод бисопряженных градиентов; bicgstab - стабилизирующий метод бисопряженных градиентов; cgs - квадратичный метод сопряженных градиентов; eigs - команда, находящая несколько собственных векторов и собственных значений; gmres - обобщенный метод минимальных остатков; pcg - метод предобусловленных сопряженных градиентов; qmr - метод квазиминимальных остатков; svds - команда, находящая несколько сингулярных значений.
Обработка, анализ и визуализация данных
Matlab включает широкий набор функций для экспорта, импорта, обработки и анализа данных. Данные сохраняются в виде столбцов или матриц чисел и могут быть загружены командой load <имя файла>.
С помощью команд, входящих в основную библиотеку Matlab, данные можно сортировать (команда sort), находить максимальное (max), минимальное (min) и среднее (mean) значение, а также стандартную дисперсию (std), сумму (sum) и произведение (prod), вычислять приближенное значение интеграла (trapz - метод трапеций) и производной (diff) и т. д.
Команды статистической обработки включают нормализацию данных, нахождение ковариационной матрицы для массива данных, коэффициентов корреляции, аппроксимацию данных полиномами и другими функциями, в том числе множественную регрессию и фильтрацию данных.
Ряд команд предназначен для Фурье-анализа (дискретное одномерное и многомерное, прямое и обратное быстрое преобразование Фурье).
Например, командой
[C=cov(A)]
[C =
0.0892 0.0330 0.0405 0.0253
0.0330 0.1505 -0.0186 0.0931
0.0405 -0.0186 0.0305 0.0056
0.0253 0.0931 0.0056 0.1112]
находим ковариационную матрицу C от переменных, являющихся столбцами матрицы A, а командой
[D=sqrt(diag(C))]
[D =
0.2987
0.3879
0.1747
0.3335]
находим вектор стандартных дисперсий.
Новая версия дополнена следующими функциями статистического анализа данных: convhull - выпуклая оболочка; cumtrapz - накопительное численное интегрирование методом трапеций; delaunay - триангуляция Делоне; dsearch - поиск ближайшей точки; factor - разложение на простые множители; inpolygon - определение точек внутри многоугольной области; nchoosek - число сочетаний n элементов по k; perms - число перестановок; polyarea - площадь многоугольника; primes - список простых чисел; sortrows - сортировка строк в возрастающем порядке; tsearch - поиск замкнутой триангуляции Делоне; voronoi - диаграмма Вороного.
Имеется несколько профессиональных приложений, которые содержат команды, расширяющие функциональные возможности Matlab по обработке данных: Optimization, Signal Processing, Spline, Statistics, Sistem Identification, Wavelet.
Разработка алгоритмов в среде Matlab
Язык Matlab - это высокоуровневый матричный язык с условными утверждениями, функциями, структурами данных, вводом-выводом и возможностью объектно-ориентированного программирования. Он обеспечивает как интерактивное программирование для быстрого создания небольших программ, так и углубленное - для создания больших и сложных программ-приложений.
Рабочая среда Matlab представляет собой набор инструментов и средств, с которыми взаимодействует пользователь программы. В нее входят средства для управления переменными, импорта и экспорта данных, а также для разработки, управления и отладки программ, написанных на языке Matlab.
Графическая система Matlab включает высокоуровневые команды для двухмерной и трехмерной визуализации данных, обработки изображений, анимации и рисования графиков, а также низкоуровневые команды, которые позволяют полностью настроить вид графиков и построить графический пользовательский интерфейс Matlab-приложения.
Как уже упоминалось, среди модулей Matlab есть многофункциональный отладчик (рис. 3) с текстовым редактором, позволяющий эффективно программировать процедуры Matlab.
Для создания процедуры Matlab достаточно записать текст программы в текстовом редакторе. Эта запись сохраняется в виде неформатированного текстового файла с расширением .m, который вызывается из командной строки или из другого m-файла.
Нужно отметить, что существует два типа m-файлов: script-файл, не требующий ввода или возврата аргументов, и функциональный m-файл, для которого необходимо и то и другое.
Script-файл оперирует в рабочей среде Matlab и используется для многократного повторения шагов вычислений.
Функциональный m-файл нужен для расширения языка Matlab, в частности, новыми алгоритмами. В оглавлении этого файла должно стоять ключевое слово - function, за которым следует название функции, например, как изображено на рис. 3. Функциональный m-файл при первом вызове автоматически компилируется.
В m-файл можно ввести строки, поясняющие его назначение и порядок использования. Эти строки начинаются с символа “%”, а на дисплей могут вызываться командой help <имя m-файла>.
Язык Matlab оперирует шестью типами данных, включая матрицы чисел, знаков, ячеек и структур. Элементами массива ячеек могут быть другие массивы. Массивы ячеек объединяют связанные данные различных типов и различного размера. Массивы структур содержат имена полей, которые, в свою очередь, содержат другие массивы. Подобно массивам ячеек, массивы структур объединяют связанные данные информации.
Матрицы чисел бывают двух типов: с числами двойной точности (они могут быть разреженными) и восьмиразрядные; последние в основном используются с приложением Image Processing.
По умолчанию любой объект Matlab считается двухмерным массивом (матрицей) чисел двойной точности.
Для написания циклов и условных переходов в Matlab имеются операторы, аналогичные языкам Фортран или Бейсик. В то же время, поскольку можно использовать в качестве переменных цикла матрицы, сами процедуры во многих случаях получаются более компактными и эффективными.
Язык Matlab позволяет вводить пользовательские типы данных, создавать и оперировать объектами, иначе говоря, он обеспечивает объектно-ориентированное программирование.
Кроме того, система Matlab имеет функции управления памятью в процессе выполнения процедур.
В состав программы входит библиотека (Application Program Interface, API), которая позволяет создавать программы на языках Си и Фортран, взаимодействующие с Matlab (MAT-файлы). Есть средства вызова подпрограмм из Matlab (динамические связи), вызова Matlab как вычисляющего процессора, а также средства чтения MAT-файлов.
Что нового
Среди усовершенствований программного языка Matlab версии 5.0 можно отметить следующие. Во-первых, добавлены многомерные массивы данных, новые функции для операций с многомерными массивами; введены новые типы данных - массивы ячеек и структур, а также команды для создания этих объектов и оперирования ими. Во-вторых, символьные массивы (строки) занимают меньше памяти, поскольку используют 16 разрядов на один символ (против 64 разрядов в предыдущей версии). В-третьих, введены новые функции для операций с символьными массивами, позволяющие преобразовывать матрицы в строки, двоичный или восьмеричный формат - в десятичный и наоборот, объединять строки в горизонтальном и вертикальном направлениях, сравнивать их и находить возможные совпадения символов.
В язык также введены новые операторы условных переходов - switch, case, otherwise, - позволяющие избежать большого числа утверждений elseif в сложных ветвлениях, и кроме того, в нем повышена эффективность выражений, содержащих оператор if. Для операций с новыми структурами данных - массивами ячеек и структур - добавлены новые логические операторы, а для операций с m-файлами - дополнительные команды, позволяющие добавить или изменить каталог для поиска файлов, ввести m-файл в редактор отладчика, присвоить или вычислить значение переменной в рабочей среде и т. п.
Заключение
С появлением программ, обобщающих накопленные знания по алгоритмам и методам решения математических задач, среди которых, безусловно, одно из лидирующих мест занимает система Matlab компании MathWorks, стало возможным решать многие задачи в совершенно не связанных между собой областях знаний одними и теми же методами.
Такие программы позволяют также по-иному построить план обучения специалистов: вначале преподавать общие методы решения задач, а лишь затем переходить к специальным задачам. Эта методика, широко применяемая сейчас на Западе, дает специалистам широкий кругозор, делает их знания более универсальными.
Хотелось бы обратить внимание преподавателей российских высших учебных заведений на замечательную программу Matlab компании MathWorks, изучив которую, выпускники - научные работники, инженеры, экономисты - вполне смогут на равных конкурировать с западными специалистами.
К сожалению, за рамками нашей статьи остался широкий спектр областей применения Matlab, включающий численное моделирование самых разных научных, технических и экономических задач. Об этих областях применения и разработанных специально для них профессиональных приложениях Matlab мы расскажем в одном из следующих номеров PC Week/RE.
В заключение хочу поблагодарить директора корпорации Softline Игоря Боровикова за любезно предоставленную возможность ознакомиться с программой Matlab 5.1