Тимофей Струнков
О чем эта статья
За последние 10 лет вышло множество книг и популярных статей, описывающих как внутреннее строение нейронных сетей, так и возможности их использования в различных областях. Тем не менее даже в среде профессионалов, имеющих дело с задачами обработки данных, встречаются существенно различные мнения о возможностях нейросетевых технологий. В этом можно убедиться, заглянув, например, на любой интернетовский форум аналитиков или трейдеров.
И это легко объяснить - ведь обработкой данных, как правило, занимаются люди с аналитическим складом ума, привыкшие к логичным и доказательным объяснениям. И их не удовлетворяют утверждения производителей нейросетей, например, “нейросети имитируют деятельность мозга”, или “нейросети успешно используются для распознавания образов”, или “нейросети позволяют обнаруживать сложные зависимости”.
Все эти формулировки имеют в основном рекламный характер и ничего не говорят о теоретической основе нейросетевого подхода. Тем не менее их нельзя назвать лживыми, так как каждая из них отражает определенный математический или биологический факт. Считается, что точное изложение этих фактов слишком сложно и неуместно в разговоре с неспециалистом (возникает ситуация “мы-то знаем, но вам не скажем”). На самом деле сущность теории нейросетей довольно проста и не требует специального образования для понимания ее задач и результатов. В данной статье мы попытаемся кратко и достаточно строго изложить один из наиболее красивых результатов теории, способный объяснить истинный смысл приведенных выше утверждений.
Вначале мы кратко опишем, каким образом формализуется одна из важнейших практических задач - поиск зависимостей. Человеческий мозг решает ее посредством передачи импульсов между нейронами. Ниже будут описаны принципы работы биологических нейронов и рассказано, как строится математическая модель нейрона, а из этих нейронов мы составим схему простейшей нейросети, пригодной для практического использования - трехслойного перцептрона. Наконец, мы поговорим о возможностях перцептрона, которые, оказывается, связаны с одной из классических проблем Гильберта и с несколькими фундаментальными теоремами математики.
Язык функций
Один из важнейших законов природы - наличие зависимостей между различными явлениями и факторами. Алиса, попав в Страну Чудес, вовремя припомнила одну такую зависимость: “Если выпить из пузырька, на котором написано "Яд", то рано или поздно почувствуешь легкое недомогание”. Подобные законы могут выражаться в различных формах. Мы будем говорить лишь об одном, наиболее строгом способе выражения зависимости, а именно в виде функции от нескольких переменных. Например, если ваш начальный вклад в швейцарском банке составлял S франков, а процентная ставка банка - h процентов годовых, то через N лет на счету окажется K = (1 + h)N · S франков, - вот типичный пример зависимости, выраженной в виде функции от трех переменных K(S, h, N).
К сожалению, задачи, в которых известен точный вид зависимости, на практике встречаются крайне редко. Рассмотрим, например, задачу оценки стоимости квартиры. Зная общую и жилую площадь квартиры, число комнат, район, удаленность от метро, тип дома и другие параметры, можно (имея некоторый опыт) вычислить ее примерную стоимость. Об опыте здесь упомянуто не зря: именно на основе личного опыта человек мысленно конструирует функцию зависимости цены от нескольких параметров, а затем вычисляет значение этой функции (на наборе показателей данной квартиры). Говоря на языке математики, для решения этой задачи нужно сделать следующее.
1. Обозначить параметры квартиры в виде переменных (x1, x2, ..., xn) и выбрать шкалы измерений. Например, район расположения квартиры можно характеризовать числом от 0 до 100, которое будет означать степень его престижности.
2. На основе нескольких десятков примеров совершенных сделок по продаже квартир построить функцию F(x1, x2, ..., xn), которая даст значение, близкое к реальной стоимости квартиры в каждой сделке. Конечно, эта функция должна быть вычислимой для любой квартиры, причем цены похожих по всем параметрам квартир должны быть близкими.
3. Теперь, определив параметры любой квартиры, мы можем подставить их в формулу нашей функции, считая полученное число оценкой стоимости квартиры. Если расхождение с истинной стоимостью окажется слишком велико, это будет означать, что рассмотренные нами ранее примеры сделок недостаточно полно характеризуют цену квартиры - либо есть какие-то важные, не учтенные нами параметры (например, шумность улицы), либо мы рассмотрели недостаточное число сделок.
Приближенные функциональные зависимости очень часто присутствуют в реальных задачах. Так, например, потребление энергии в частном секторе описывается функцией, зависящей от времени года, температуры воздуха, силы ветра, влажности, облачности и других известных параметров. В основе технического анализа рынков лежит утверждение, что завтрашняя цена является функцией от нескольких предыдущих цен, значений различных индикаторов и некоторых макроэкономических показателей. Ясно, что эти функции невозможно определить априори, в отличие от функции капитала в швейцарском банке. Ясно также, что эти функции записываются достаточно сложными формулами неизвестного вида, в которых участвуют все переменные. Имеет смысл решать задачу подбора подходящей функции, если известны значения этой функции в некоторых точках. Похожими задачами, в принципе, занимается статистика, однако существенный прогресс в их решении достигнут лишь в некоторых случаях (например, для оценки линейных функций). Поэтому для нахождения зависимостей активно разрабатываются и другие подходы, в том числе и технология нейронных сетей.
Если до сих пор поиск зависимостей мы осуществляли с помощью собственного мозга, а теперь хотим хотя бы частично автоматизировать этот процесс, то, естественно, возникает идея - смоделировать деятельность мозга в некотором автомате и заставить его работать на наших числовых данных. Развитию этой идеи и рассказу о функционировании мозга посвящен следующий раздел.
Биологические нейроны
Так как на эту тему написано уже много популярных статей, остановимся лишь на основных принципах строения и функционирования биологических нейронов. Вот эти принципы.
1. Основную роль в деятельности нервной системы и мозга животных играют специальные клетки - нейроны, связанные между собой нервными волокнами. Нейроны могут посылать друг другу электрические импульсы - сигналы различной силы и частоты.
2. Нейрон состоит из дендритов (по ним принимаются сигналы от других нейронов), тела нейрона (оно обеспечивает жизнедеятельность всей клетки) и аксона (это длинная нить, по ней нейрон может передавать сигналы другим нейронам). Аксон контактирует с дендритами других нейронов посредством специальных образований - синапсов, которые влияют на силу сигнала. Таким образом, синапсы можно считать входами нейрона.
3. Сигналы, полученные нейроном от нескольких других нейронов одновременно, суммируются. Если сила суммарного сигнала превышает некоторое пороговое значение (важна также длительность сигнала), то нейрон возбуждается, генерирует собственный импульс и передает его по аксону.
Биологическая нейронная теория очень развита и сложна. Чтобы построить математическую модель процессов, происходящих в мозгу, мы вынуждены принять несколько предположений:
1) будем считать, что каждый нейрон обладает некоторой передаточной функцией, определяющей условия его возбуждения в зависимости от силы полученных сигналов. Предполагается, что передаточные функции не зависят от времени;
2) при прохождении синапса сигнал меняется линейно, т. е. сила сигнала умножается на некоторое число. Это число мы будем называть весом синапса или весом соответствующего входа нейрона;
3) деятельность нейронов синхронизирована, т. е. время прохождения сигнала от нейрона к нейрону фиксированно и одинаково для всех связей. То же самое относится к времени обработки принятых сигналов.
Заметим, что веса синапсов могут меняться со временем - это принципиальная особенность. Именно изменение этих весов отвечает за возможность различной реакции организма на одни и те же условия в разные моменты времени, т. е. возможность обучения.
Нужно признать, что все эти предположения достаточно сильно огрубляют биологическую картину. Например, время передачи сигнала напрямую зависит от расстояния между нейронами (оно может быть достаточно большим). Тем удивительнее, что при этих огрублениях полученная модель сохраняет некоторые важные свойства биологических систем, в том числе адаптивность и сложное поведение.
Математический нейрон
Построим математическую модель нейрона (далее мы будем называть ее нейроном). Нейрон - это несложный автомат, преобразующий входные сигналы в выходной сигнал. Сигналы силы x1, x2, ..., xn, поступая на синапсы, преобразуются линейным образом, т. е. к телу нейрона поступают сигналы силы w1x1, w2x2, ..., wnxn (здесь wi - веса соответствующих синапсов). Для удобства к нейрону добавляют еще один вход (и еще один вес u), считая, что на этот вход всегда подается сигнал силы 1. Нейрон суммирует эти сигналы, затем применяет к сумме некоторую фиксированную функцию p и выдает на выходе сигнал силы y = p(w1x1 + + w2x2 + ... + wnxn + u).
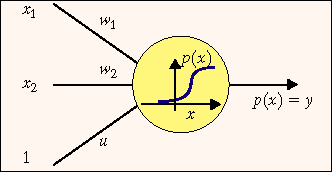
Рис.1. Математический нейрон
Эта модель была предложена Маккалоком и Питтсом еще в 1943 г. При этом использовались пороговые передаточные функции (рис. 2a), и правила формирования выходного сигнала y выглядели особенно просто: если w1x1 + w2x2 + + ... + wnxn + u і T, то y = 1, иначе y = 0.

Рис. 2. Передаточные функции нейронов: а) пороговая; б) сигмоидная
В 1960 г. на основе таких нейронов Розенблатт построил первый в мире автомат для распознавания изображений букв, который был назван “перцептрон” (perception - восприятие). Этот автомат имел очень простую однослойную структуру и мог решать только относительно простые (линейные) задачи. С тех пор были изучены и более сложные системы из нейронов, использующие в качестве передаточных любые непрерывные функции. Одна из наиболее часто используемых передаточных функций называется сигмоидной (или логистической) и задается формулой s(x) = 1/(1 + e-x) (см. рис. 2б).
Нейронная сеть
Нейронная сеть - это набор нейронов, определенным образом связанных между собой. В качестве основного примера рассмотрим сеть, которая достаточно проста по структуре и в то же время широко используется для решения прикладных задач - трехслойный перцептрон с n входами и одним выходом.
Как следует из названия, эта сеть состоит из трех слоев, изображенных на рис. 3. Собственно нейроны располагаются во втором (скрытом) и в третьем (выходном) слое. Первый слой только передает входные сигналы ко всем H нейронам второго слоя (здесь H = 4). Каждый нейрон второго слоя имеет n входов, которым приписаны веса wi1, wi2, ..., win (для нейрона с номером i). Получив входные сигналы, нейрон суммирует их с соответствующими весами, затем применяет к этой сумме передаточную функцию и пересылает результат на один из входов нейрона третьего слоя. В свою очередь, нейрон выходного слоя суммирует полученные от второго слоя сигналы с некоторыми весами ni. Для определенности будем предполагать, что передаточные функции в скрытом слое являются сигмоидными, а в выходном слое используется функция p(x) = x, т. е. взвешенная сумма выходов второго слоя и будет ответом сети.
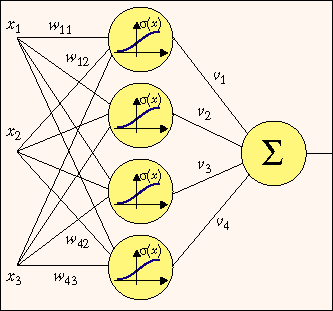
Рис. 3. Трехслойный перцептрон
Итак, подавая на входы перцептрона любые числа x1, x2, ..., xn, мы получим на выходе значение некоторой функции F(x1, x2, ..., xn), которое является ответом (реакцией) сети. Очевидно, что ответ сети зависит как от входного сигнала, так и от значений ее внутренних параметров - весов нейронов.
Выпишем точный вид этой функции:
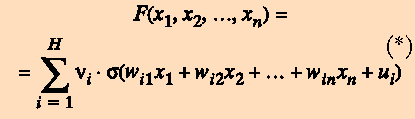
Как видно из этого равенства, такой перцептрон реализует только функции определенного вида, а именно суммы значений сигмоидных функций, где в качестве аргументов подставляются линейные комбинации входных сигналов. Например, функцию F(x1, x2) = = x1x2 не удается с ходу представить в таком виде.
Естествен вопрос: а может ли перцептрон реализовать достаточно сложную функцию? Этот вопрос по сути чисто математический - о представимости одних функций посредством других. Так как задача очень просто сформулирована, неудивительно, что и занимались ею ученые достаточно давно. Удивительно то, что ответ на нее был получен сравнительно недавно - в 1989 г. Формулировке этого ответа посвящены следующие два раздела.
Тринадцатая проблема Гильберта
На несколько минут обратимся к самым что ни на есть фундаментальным вопросам математики.
В 1900 г. гениальный немецкий математик Давид Гильберт в своем докладе на Международном конгрессе математиков в Париже сформулировал 23 нерешенные задачи, которые он считал наиболее важными в математике того времени. Эти задачи получили название “проблемы Гильберта” и оказали огромное влияние на развитие всей математики XX века. До сих пор не все проблемы Гильберта полностью решены, а многие из них побудили ученых к созданию совершенно новых теорий. Как выяснилось в последние годы, теория нейронных сетей также связана с одной из этих проблем, а именно с тринадцатой. Тринадцатую проблему Гильберта можно сформулировать так.
Верно ли, что существует непрерывная функция от трех переменных, которая не может быть представлена в виде композиции непрерывных функций от двух переменных?
Под композицией функций понимается подстановка одной функции в качестве аргумента другой. Например, функция трех переменных F(x, y, z) = xz + yz может быть представлена в виде композиции функций двух переменных F(x, y, z) = S(M(x, z), M(y, z)), где M(x, z) = xz, а S(a, b) = a + b.
Тринадцатая проблема Гильберта была решена в 1957 г. тогдашним студентом мехмата МГУ, а ныне академиком Владимиром Игоревичем Арнольдом. Он показал, что любая непрерывная функция трех переменных представляется в виде композиции непрерывных функций двух переменных. Таким образом, гипотеза Гильберта была опровергнута.
В том же 1957 г. советский математик Андрей Николаевич Колмогоров доказал гораздо более сильную теорему.
Теорема Колмогорова. Любая непрерывная функция от n переменных F(x1, x2, ..., xn) может быть представлена в виде
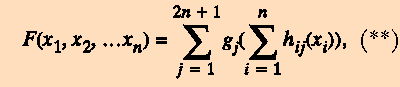
где gj и hij - непрерывные функции, причем hij не зависят от функции F.
Эта теорема означает, что для реализации функций многих переменных достаточно операций суммирования и композиции функций одной переменной. Удивительно, что в этом представлении лишь функции gj зависят от представляемой функции F, а функции hij универсальны.
Заметим, что формула (**) очень похожа на формулу (*). Если перевести эту теорему на язык нейросетей, то она будет звучать так.
Если известны функции hij, то любую непрерывную функцию от n переменных можно точно реализовать с помощью простой нейросети на основе трехслойного перцептрона. Для этого достаточно подобрать 2n+1 передаточных функций gj нейронов скрытого слоя.
Эта сеть не будет перцептроном в строгом смысле, так как на входах второго слоя к сигналам необходимо применить функции hij, а не просто умножить их на веса.
К сожалению, при всей своей математической красоте, теорема Колмогорова малоприменима на практике. Это связано с тем, что функции hij - негладкие и трудно вычислимые; также неясно, каким образом можно подбирать функции gj для данной функции F. Роль этой теоремы состоит в том, что она показала принципиальную возможность реализации сколь угодно сложных зависимостей с помощью относительно простых автоматов типа нейронных сетей.
Аппроксимация нейронными сетями
Чтобы получить более значимые для практики результаты в этом направлении, приходится ослабить наши требования. Во-первых, для нас непринципиально найти точное представление данной функции - достаточно иметь приближенное. Во-вторых, мы можем по необходимости увеличивать число нейронов в скрытом слое, насколько это требуется. Новый вариант теоремы Колмогорова, обладающий этими особенностями, был открыт только в 1989 г., зато одновременно несколькими авторами. Так как все эти работы стали классическими, дадим точные ссылки.
1. Hornick, Stinchcombe, White. Multilayer Feedforward Networks are Universal Approximators. Neural Networks, 1989, v. 2, № 5.
2. Cybenko. Approximation by Superpositions of a Sigmoidal Function. Mathematical Control Signals Systems, 1989, 2.
3. Funahashi. On the Approximate Realization of Continuous Mappings by Neural Networks. Neural Networks, 1989, v. 2, № 3.
Для определенности сформулируем теорему в том виде, в каком она приведена во второй из названных работ.
Пусть F(x1, x2, ..., xn) - любая непрерывная функция, определенная на ограниченном множестве, и e > 0 - любое сколь угодно малое число, означающее точность аппроксимации. Через s мы обозначаем сигмоидную функцию, определенную выше.
Теорема. Существует такое число H, набор чисел wij, ui и набор чисел ni, что функция приближает данную функцию F(x1, x2, ..., xn) с погрешностью не более e на всей области определения.
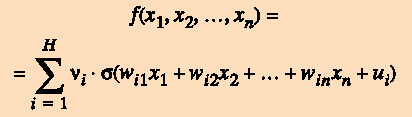
Читатель легко заметит, что эта формула полностью совпадает с выражением (*) для функции, реализуемой перцептроном. В терминах теории нейросетей эта теорема формулируется так.
Любую непрерывную функцию нескольких переменных можно с любой точностью реализовать с помощью обычного трехслойного перцептрона с достаточным количеством нейронов в скрытом слое.
О рекламе в индустрии нейросетей
Настало время обсудить, насколько сильно лукавят производители нейросетей, расхваливая достоинства этой технологии. Также обсудим несколько стандартных клише, которые часто встречаются в популярных статьях.
“Нейросети имитируют деятельность мозга” - это верно лишь отчасти. В современной биологии нет единой точки зрения на механизмы действия мозга. Однако нейросети обладают определенными биологическими чертами (такими, как параллельность обработки информации в нейронах и адаптивность), которые все же делают эту фразу уместной.
“Нейросеть - это черный ящик”. Справедливое в целом утверждение, отражающее важный недостаток нейросетевого подхода - неинтерпретируемость результатов. Ответ сети - сложная нелинейная функция от входных значений, и поэтому непросто понять, какими особенностями входного примера обусловлена реакция сети. Для анализа нейронных сетей существует специальное программное обеспечение, которое иногда позволяет справиться с этой проблемой. Однако заметим, что во многих практических задачах интерпретация не столь важна, как сам результат. Например, это относится к задачам распознавания речи, сжатия и распознавания изображений и многим другим. В этой связи утверждение, что “нейросети успешно используются для распознавания образов”, полностью обосновано. В литературе можно найти тому множество конкретных примеров из области техники, медицины и т. д.
“Нейросети позволяют обнаруживать сложные зависимости”. Это утверждение в литературе формулируется и в таком виде: “нейросети являются универсальными аппроксиматорами”, что в точности соответствует приведенной выше теореме 1989 г. Оно означает, что с помощью стандартного перцептрона в принципе возможно решать любые задачи прогнозирования и оценки, в которых существуют функциональные зависимости. Мы говорим “в принципе”, так как эта теорема не указывает, каким способом можно подобрать веса каждого нейрона, используя набор примеров. Процесс подбора весов называется обучением нейронной сети. Настоящим прорывом в теории обучения нейронных сетей стало открытие в 1986 г. метода обратного распространения ошибки (error back-propagation). Ныне этот метод очень широко используется в различных приложениях, однако он требует настройки нескольких параметров обучения и не всегда приводит к оптимальному результату. Поэтому нужно четко понимать, что хотя нейросеть и является механизмом, способным решить широкий класс задач, но правила управления этим механизмом пока что находятся на уровне догадок и эвристических соображений. Многие крупные фирмы и частные лица имеют собственные разработки в этой области, однако они не торопятся обнародовать их, предпочитая получать доход от непосредственного использования своих систем.
“Нейросети способны к самообучению”. Это утверждение многие трактуют неправильно. Хотя алгоритм обучения (например, методом обратного распространения) - автоматическая процедура, это не означает, что пользователю совсем не придется думать, применяя технологию нейросетей. Требуется грамотно готовить данные, выбирать тип сети, подстраивать различные параметры и учиться интерпретировать результаты - только тогда нейросеть станет действительно полезным инструментом.
“Нейросети способны корректно действовать в совершенно новых ситуациях” - утверждение, не лишенное основания. Например, нейросетевые системы распознавания речи могут достаточно качественно воспринимать речь диктора, голос которого система никогда не слышала ранее. Однако речь - довольно специфичный объект, и это утверждение нельзя безоговорочно распространять на любые задачи. Бессмысленно, например, предсказывать финансовый кризис, если в процессе обучения сети ей не было предъявлено ни одного примера кризисной ситуации.
Как видим, ситуация с нейронными сетями далеко не однозначна. Мы рассмотрели лишь два аспекта - связь с биологическими нейронами и возможности перцептрона, почти не коснувшись других не менее важных и интересных вопросов. Ведь кроме перцептрона существует еще несколько десятков архитектур нейросетей, каждая из которых применяется для специальных классов задач и использует свои алгоритмы обучения.
Прошло то время, когда нейронные сети представлялись необъяснимой фантастикой и ассоциировались только с модным словосочетанием “искусственный интеллект”. Сегодня нейротехнология - вполне обычный инструмент для обработки данных, достаточно сложный в освоении и использовании, но эффективный для определенного класса задач, причем список этих задач постоянно растет. Благодаря наличию солидной теоретической базы можно быть уверенным, что в скором будущем нейросетевые продукты получат самое широкое распространение.
Мы не будем навязывать читателю каких-либо выводов - делать их не столько рано, сколько бессмысленно в вопросах применения новых технологий. Все зависит от решаемых задач, способности пользователя к восприятию нового, допустимого времени окупаемости затрат и многих других факторов.
С автором статьи можно связаться по адресу: tim@mics.msu.su.