Анализ по 16 показателям пяти современных интегрированных математических систем для ПК: Derive (под MS-DOS), MathCAD PLUS 6.0, Maple V R3, Mathematica 2.2.2 и MatLAB 4.2 под Windows.
От электронных "счетов" к символьной математике
В такой традиционной сфере применения ПК, как математические расчеты, в последние годы наметился огромный прогресс. Появилось большое число интегрированных математических систем как для численных, так и для аналитических (символьных) вычислений. В данном обзоре проводится сравнительный анализ ряда математических систем, получивших распространение у пользователей во всем мире, в том числе и в России:
- Derive 2.6 фирмы Soft Warehouse;
- MathCAD PLUS 6.О для Windows фирмы MathSoft;
- Maple V R3 для Windows фирмы Waterloo Maple Software;
- Mathematica 2.2.2 для Windows фирмы Wolfram Research;
- MatLAB 4.0/4.2 для Windows фирмы MathWorks.
Первые четыре системы относятся к новейшим пакетам символьной математики (компьютерной алгебры). MatLAB 4.0/4.2 (рис. 1) - матричная система, ориентированная на сложные численные вычисления. Однако к ней отдельно выпускается расширение символьной математики, что наряду с реализацией под Windows делает систему применимой для самых серьезных математических вычислений.
Аппаратные ресурсы
Аппаратные ресурсы перестали быть главным показателем в оценке программных систем. Тем не менее экономия системных ресурсов - важное достоинство систем:
Стоимость систем
Цены стандартных комплектов поставки систем, по данным журнала Software for Science и корпорации SoftLine, реализующей программные продукты научного назначения в России, следующие: Derive 2.6 - $250, MathCAD PLUS 6.0 - $495, Maple V R3 - $695, Mathematica 2.2.2 - $995, MatLAB 4.2 - $2120.
Можно сделать любопытный вывод - возможности систем впрямую не зависят от их стоимости. Так, самой дорогой является система MatLAB, хотя в стандартной комплектации она вообще лишена функций символьных вычислений.
Полнота ядра символьных операций
Под полнотой ядра следует понимать число встроенных в ядро функций и алгоритмов символьных преобразований. Такого ядра вообще нет у системы MatLAB. Она способна выполнять сложнейшие численные расчеты и обрабатывать большие массивы данных (рис. 1).
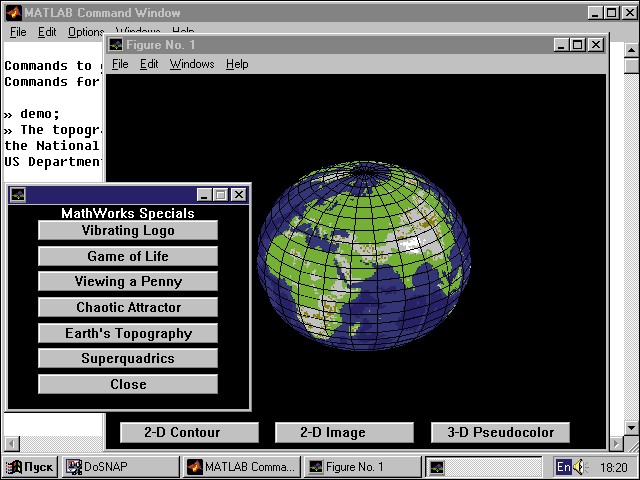
Рис. 1. Матричная система MatLAB 4.0/4.2 способна выполнять сложнейшие расчеты,
например строить карту по данным топографических обмеров
Ядро MathCAD PLUS 6.0 - это сильно сокращенная версия ядра Maple V. В целом MathCAD, хотя она и прорвалась в ряды систем компьютерной алгебры, все еще остается системой "для всех", ориентированной скорее на численные расчеты, чем на символьные (рис. 2).
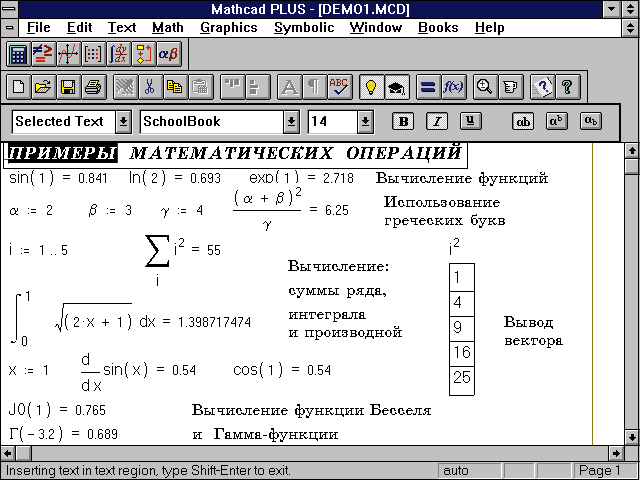
Рис. 2. Система MathCAD PLUS 6.0 с естественным математическим входным языком
удобна для выполнения повседневных расчетов
Лидером по полноте ядра является система Maple V5 - в ее ядре около 2800 различных функций (включая модификации). Неплохо представлены и алгоритмы математических преобразований. Такое обилие функций и правил преобразования математических выражений свидетельствует о мощи этой системы в решении задач компьютерной алгебры.
Достаточно полным является и ядро системы Mathematica 2.2.2. В нем есть даже функции для решения серьезных экономических задач (рис. 3). Однако по числу функций (около 800 не считая слов-определений) эта система все же уступает Maple V R3.
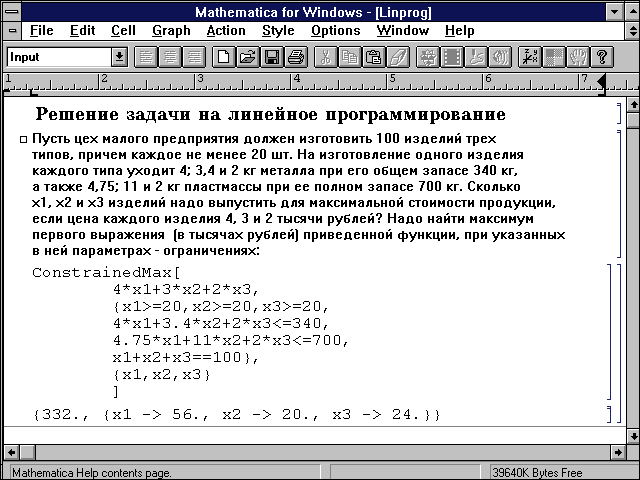
Рис. 3. Решение экономической задачи методом линейного программирования
с помощью одной из функций ядра системы Mathematica 2.2.2
Ядро Derive прекрасно работает с элементарными функциями, но не имеет многих специальных математических функций. Поэтому на фоне потрясающего роста возможностей символьной математики у таких монстров, как Mathematica 2.2.2 и Maple V R3, возможности Derive сейчас можно оценить как довольно скромные. Хотя блестки гениальности она проявляет довольно часто. Это следствие реализации системы на специальной версии языка LISP.
Полнота системы
Под полнотой системы будем подразумевать ее возможности с учетом возможностей не только ядра, но и всех внешних библиотек и прикладных пакетов.
Maple V R3 и Mathematica 2.2.2 имеют богатейшие библиотеки, заслуживающие высшей оценки. Куда скромнее библиотеки Derive, хотя и они впечатляют богатством функций. MathCAD проигрывает из-за того, что прикладные пакеты этой системы поставляются отдельно и стоят довольно дорого - от $75 до $99. Их нельзя считать органической составляющей системы. Хотя по обилию и разнообразию библиотек, организованных в форме электронных книг, эта система является непревзойденной.
Система MatLAB 4.0/4.2 поражает легкостью своего расширения - достаточно задать новую функцию, как она становится доступной для дальнейшей работы без какого-либо последующего доопределения. Этот пакет - подлинный кладезь возможностей для любителей создавать свои собственные математические системы (прежде всего для операций с векторами и матрицами).
Производительность выполнения простых операций
Наивысшей оценки по этому показателю заслуживает система Derive, которая почти мгновенно выдает результаты простых тестовых примеров. Довольно резвой (при численных расчетах) является система MatLAB 4.0. Хорошей следует признать производительность систем MathCAD и Maple V R3. Mathematica 2.2.2 - единственная система, которая работает удручающе медленно на ПК с 4 Мб ОЗУ.
Вообще говоря, приходится с сожалением констатировать, что системы символьной математики довольно медлительны, когда речь идет об их применении в качестве "числодробилок". В этой роли они заметно уступают пакетам для численных расчетов, не говоря уже о программах, написанных на компилируемых языках программирования, таких, как Фортран, Си, Паскаль и даже Бейсик. Но не надо забывать о другом - эти системы дают поразительно точные ответы (результат имеет подчас многие тысячи верных знаков).
Достоверность решения
Достоверность решения задач компьютерной алгебры никогда не будет полной, хотя бы по причине неоднозначности многих символьных преобразований. Тем не менее все системы предлагают достаточно высокий уровень достоверности решения таких задач.
Система Maple V R3 заслуживает отличной оценки. Заметно улучшились показатели версии Mathematica 2.2.2 - большинство ее огрехов, возникавших при решении аналитических задач, удалось убрать. Однако, по крайней мере таково наше впечатление, по корректности решения задач Maple V R3 уже превзошла нынешнего лидера среди систем символьной математики - пакет Mathematica 2.
Derive по-прежнему превосходно щелкает простые задачи, в которых нет специальных математических функций. Увы, задачи, где такие функции встречаются, практически не по зубам этой системе: вместо подстановки специальных функций она выдает их громоздкие интегральные представления.
Графические возможности
Подтверждается, что чем мощнее система, тем больше графических возможностей она предоставляет. На фоне богатых других систем ущербная графика Derive не заслуживает даже удовлетворительной оценки: мало/ число типов графиков, отсутствует функциональная закраска и т. д.
Заметно улучшена графика системы MathCAD PLUS 6.0, функциональная закраска стала такой же, как у систем Maple V R3 и Mathematica 2.2.2. Последняя - бесспорный лидер по графическим возможностям. Их богатство определяется не только обилием графических функций, позволяющих строить самые разнообразные графические объекты, но и множеством опций для модификации графиков. Однако новая система Maple V R3 стремительно сокращает разрыв с лидерами по графическим возможностям (рис. 4).
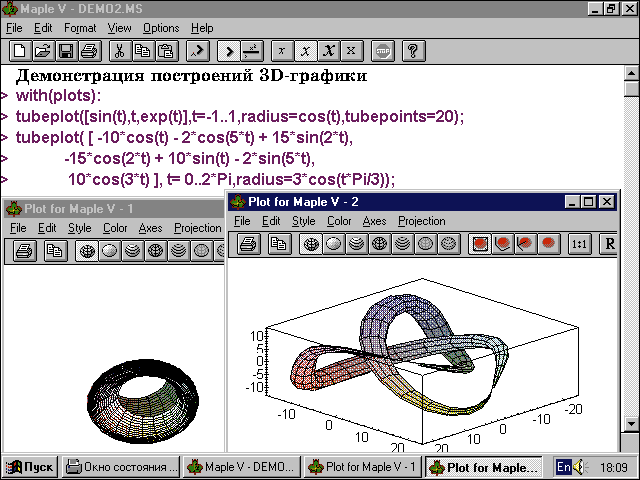
Рис. 4. Богатые графические возможности математических систем иллюстрирует
система Maple V R3
Разнообразие графических возможностей заметно расширяет сферы применения математических систем. Особенно отрадно отметить, что большинство из них может строить высококачественные графики по умолчанию. И лишь когда необходимо придать им особые свойства, приходится использовать специальные опции и настройки.
Воспроизведение анимационных графиков
К новинкам математических систем, явно навеянным развитием мультимедиа, относится возможность построения анимационных графиков. Теперь, анализируя колебания струны, пластины или сложной поверхности, можно наблюдать эти колебания на экране дисплея. Кроме Derive, все рассмотренные в этом обзоре математические системы имеют средства воспроизведения анимационных графиков.
Особенно удачно анимация реализована в системах Maple V R3 и Mathematica 2.2.2, которые позволяют, например, наблюдать колебания сложных математических трехмерных поверхностей, описываемых специальными математическими функциями. К достоинствам MathCAD относится возможность воспроизведения стандартных видеофайлов .AVI. Хотя это, может быть, и не имеет прямого отношения к математике.
Синтез и воспроизведение звука
Еще одним новым качеством математических систем становится воспроизведение звуковых сигналов, например для озвучивания колебаний, взрывных процессов и т. д. Пока лишь две системы, Mathematica 2.2.2 и MatLAB 4.2, включают эту функцию. Mathematica 2.2.2 воспроизводит звуки, описываемые математическими формулами, а MatLAB 4.2 неплохо воспроизводит и некоторые звуковые файлы.
Но ни одна из этих систем не позволяет выполнять серьезное редактирование звуковых файлов и воспроизводить все их форматы.
Интерфейс пользователя
Под интерфейсом пользователя мы подразумеваем средства, делающие работу с системой интуитивной и наглядной. Это относится к наличию современных меню и баз данных помощи, легкости управления окнами и к возможности управления мышью. По пятибалльной шкале интерфейсы систем можно оценить следующим образом: Derive 2.06 - 2; MatLAB 4.2 - 3; Mathematica 2.2.2 - 4; MathCAD PLUS 6.0 - 5; Maple V R3 - 5.
Интерфейс MathCAD PLUS 6.0 заслуживает самой высокой оценки. Это единственная система, обеспечивающая подготовку документов в подлинно математическом виде в стиле Notebook (блокнот), сочетая тексты, формулы, таблицы и графики (рис. 5). Интерфейс системы приобрел типичные черты интерфейса 32-разрядных приложений Windows 95 - имеется множество пиктограмм быстрого управления, селекторы спецзнаков, переключатели шрифтов и т. д.
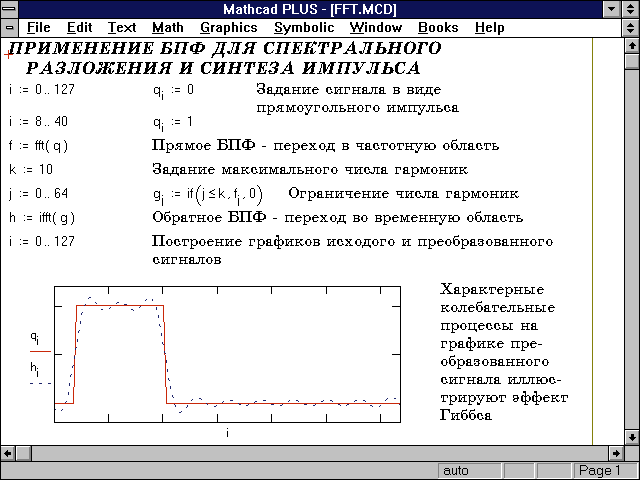
Рис. 5. Математическая система MathCAD PLUS 6.0 имеет
превосходный интерфейс
Интерфейс Maple V R3 кажется с первого взгляда простоватым: в нем нет окон с набором спецзнаков и мало пиктограмм быстрого управления. Однако результат этого сокращения оказывается неожиданным - с системой просто приятно работать (в том числе и под Windows 95). Поэтому она также заслуживает отличной оценки по данному показателю. Хотя ввод данных и задания на их выполнение производится по старинке (в командной строке), по представлению символьных результатов Maple V R3 не уступает MathCAD - результаты выводятся в естественном математическом виде (рис. 6).
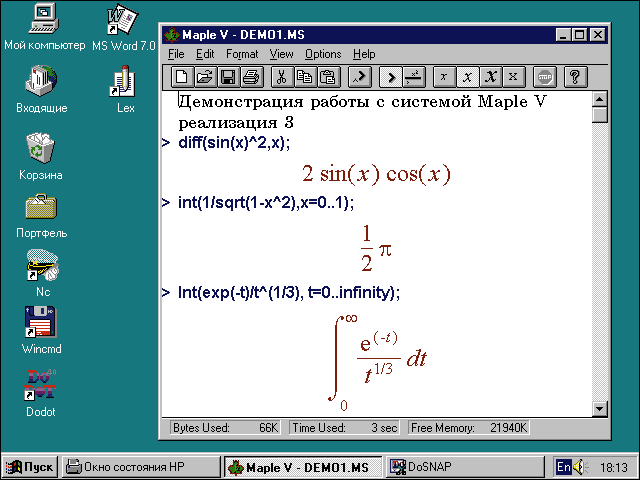
Рис. 6. Задания в системе Maple V R3 вводятся в текстовом формате,
но результаты представляются в естественном формульном виде
Реализация стиля Notebook в системе Mathematica 2 пока явно недоработана: каждая ячейка занимает полную строку, представление математических символов в естественном виде отсутствует, в пределах ячейки допустим лишь один стиль символов и комментариев. О естественности представления данных, команд и результатов вычислений не приходится и мечтать. Это послужило поводом для снижения оценки до 4 баллов. Однако следует помнить, что ущербность внешнего представления данных в ячейках Mathematica 2.2.2 порождена уникальным свойством этой системы - символьные данные в ячейках автоматически модифицируются при изменении исходных данных!
На фоне прекрасного Windows-интерфейса других систем интерфейс Derive выглядит архаически примитивным. Работу с мышью система Derive не поддерживает вообще. В целом по этому показателю система не заслуживает даже удовлетворительной оценки.
Работа в режиме калькулятора
Пользователь, купивший математическую систему, вправе рассчитывать на то, что ему не надо будет при работе с ней держать под рукой калькулятор. Однако не все так просто. Численные расчеты - подлинная обуза для систем символьной математики.
Тем не менее все системы являются превосходными калькуляторами - разумеется, куда более мощными, чем, скажем, "научный калькулятор", встроенный в оболочку Windows. Лишь система Mathematica 2.2.2 вызывает нарекания - особый синтаксис ее входного языка затрудняет проведение расчетов в общепринятом виде.
Возможности редактирования документов
В ходе сеанса работы с системой (сессии) готовятся документы, содержащие текстовые сообщения, математические формулы, рисунки и таблицы. Их приходится постоянно редактировать с целью исправления ошибок или придания документам лучшей наглядности.
Здесь хуже всего обстоят дела у системы Derive. Она имеет только простейший строчный редактор - архаичное средство, о котором многие пользователи уже давно забыли. К тому же Derive - единственная система, не поддерживающая работу с мышью.
MathCAD, напротив, по этому показателю явно лидирует, программа редактирования здесь прекрасна, и можно эффективно пользоваться мышью. В новой версии MathCAD для редактирования удобны перемещаемые по всему экрану панели с наборами всех мыслимых математических символов, а также греческих букв.
Несколько хуже эти возможности реализованы в системах Maple V R3 и Mathematica 2.2.2. Главный недостаток этих систем - невозможность написания исходных математических формул в естественном виде, что давно реализовано в системе MathCAD. MatLAB 4.0 сохранил от старой версии примитивное редактирование.
База данных помощи
Система помощи Derive крайне примитивна - это просто список команд и функций с их названиями. Никаких примеров применения функций нет, хотя их синтаксис кратко представлен. Разгадка возможностей многих функций без документации превращается в ребус.
В MathCAD PLUS 6.0, напротив, база данных помощи построена с учетом возможностей Windows. Она удобна в работе и достаточно полна. Данные из базы можно переносить в текст документов.
Система помощи Maple V R3 также выполнена с блеском. Она не отличается новациями интерфейса, но зато из ее подсказок можно вырезать любой фрагмент (например, сразу несколько тестовых примеров или целую программу), перенести его в рабочее окно и тут же исполнить. При этом по обилию примеров Maple V R3 намного обходит другие системы. База данных помощи содержит несколько примеров по каждой функции, их общее число превышает 10 тысяч!
Справочная система Mathematica 2.2.2 выполнена вполне добротно и современно. Но число примеров применения функций в базе данных помощи этой системы мало, а на многие функции примеров просто нет. MatLAB 4.0 сохранила архаичную и примитивную, но довольно полную базу данных помощи.
Практические примеры (прикладные пакеты)
При освоении систем немаловажное значение имеет наличие практических примеров применения систем. Речь идет о дополнительных примерах, не включенных в базу данных помощи.
Примеры для Mathematica 2.2.2 даны в виде файлов в каталоге Notebook. Эти примеры, в первую очередь, призваны продемонстрировать мощь системы - прекрасную графику (в том числе с режимом анимации) и возможность выполнения сложных вычислений. Примеры очень сложны и нередко преднамеренно даны в режиме скрытия деталей вычислений. Разобраться с ними довольно сложно.
Радует обилием практических примеров система Maple V R3. Многие из них подготовлены в виде проблемных математических статей и наглядно демонстрируют огромные возможности этой системы: от простых численных расчетов с идеальной точностью до решения в символьном виде систем дифференциальных уравнений.
В системе MathCAD имеется обширный набор коротеньких примеров, названных Quick Sheets. Как и в системе Maple, эти примеры охватывают обширный набор математических понятий, их можно модифицировать и приспосабливать для своих целей.
Но поистине уникальна возможность создания для MathCAD 6.0 "живых" книг, содержащих тексты, формулы, графики и анимационные изображения и работающих с любыми вводимыми пользователем данными (рис. 7). К настоящему времени выпущены десятки электронных книг для системы MathCAD: справочники по математике, физике и астрономии, книги по расчетам в механике, химии, электротехнике, радиотехнике и т. д.
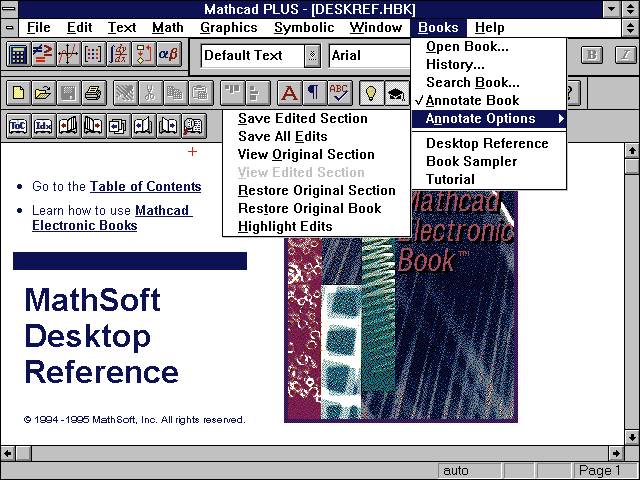
Рис. 7. Работа с электронными книгами - важное достоинство
системы MathCAD PLUS 6.0
MatLAB 4.2 содержит много полезных примеров, но всеобъемлющим их набор никак не назовешь. К тому же все они заданы в виде обычных программ, так что понять примеры можно, только изучив довольно сложный язык программирования системы.
Впрочем, дополнительно с системой MatLAB поставляется множество прикладных пакетов: SIMULINK - модуль графического моделирования функциональных систем, Symbolic Math Toolboox - символьные математические операции, MatLAB Optimization Toolboox - оптимизационные задачи, MatLAB Signal Processing Toolboox - анализ сигналов и др. К сожалению, стоимость этих дополнений (сотни долларов за каждое) довольно велика.
Немало примеров и в системе Derive. Однако они - детский лепет по сравнению с тем, что имеется в других системах. Хотя начинающие приобщаться к аналитическим вычислениям пользователи ПК наверняка найдут в примерах Derive много полезного и поучительного.
Язык программирования
Большинство математических систем сводят к минимуму необходимость программирования задач, решаемых пользователем. Однако для расширения систем, особенно опытными пользователями, в них вводят язык программирования сверхвысокого уровня, ориентированный на решение математических задач. Этот язык принято называть входным языком общения с системой.
Система Mathematica 2 включает развитый язык программирования. Он содержит полный набор управляющих структур и многочисленные средства как низкого уровня (работа с памятью и дисками), так и высокого и даже сверхвысокого уровня (обращение к любым функциям ядра). Язык программирования системы Maple V R3 не уступает ему и также превосходен.
Наконец-то приобрела подобие языка программирования система MathCAD PLUS 6.0. Она позволяет задавать свои функции с реализацией основных управляющих структур (рис. 8). Возможности этого языка довольно примитивны, но не надо забывать, что они дают как раз те средства, которых так не хватало для общения с этой системой.
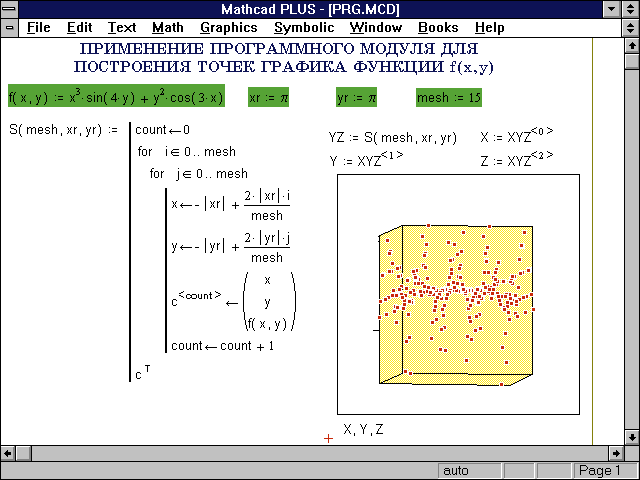
Рис. 8. Применение программных средств в сисетме MathCAD PLUS 6.0
при решении специальной графической задачи
Язык программирования MatLAB 4.2 - своеобразная смесь возможностей Фортрана, Паскаля и Бейсика. Язык довольно мощный, но все же уступает языкам программирования Maple V R3 и Mathematica 2.2.2. Однако, как отмечалось, уникальной особенностью MatLAB была и есть простота расширения средств языка программирования системы, что делает систему расширяемой и легко адаптируемой к задачам пользователя.
Что касается Derive, то ее средства программирования находятся в рудиментарном виде и представлены буквально несколькими функциями. Однако и с помощью такого "языка" можно решать прикладные задачи.
Безаварийность работы
Безотказность математических систем выглядит не очень радужно. Всем системам присуще явление разбухания результатов вычислений и зацикливание работы в отдельных, слишком сложных и непосильных для них случаях. Увы, порою исходные данные оказываются обманчиво просты. Поэтому математическая образованность и интуиция пользователя имеют важнейшее значение при работе с такими системами.
Derive - довольно надежная система. Ее недостаток - отсутствие поддержки расширенной памяти современных ПК. Так что при решении сложных задач нередко появление сообщений о нехватке памяти. Версия Derive /XM свободна от этого недостатка, но пока мало распространена.
Не удалось ни разу отметить сбоев в работе систем MathCAD PLUS 6.0 и Maple V R3. Достаточно редки они и у системы MatLAB 4.0. Все это говорит о неплохой надежности этих систем.
Заметно хуже ситуация с системой Mathematica 2.2.2: у нее иногда возникали фатальные ошибки с предупреждением о выходе из сеанса работы с системой. Были и случаи зависания системы. В новой версии эти недостатки в значительной мере устранены, но все же не полностью. Поэтому системе выставлена удовлетворительная оценка*.
Итоговые выводы
Итак, мы сравнили пять современных математических систем по 16 различным показателям. Можно ожидать, что качество систем в основном определяется частными показателями (и прежде всего их основным назначением), а не какой-либо количественной суммарной оценкой. Здесь та же ситуация, что с оценками в школе, - порой из троечника вырастает академик, а круглая отличница становится домохозяйкой.
На наш взгляд, существенный прогресс характерен для системы Maple V R3 для Windows. Несомненно, что это - следствие необычно мощного ядра символьных операций в этой системе, значительно улучшенного (в сравнении с предшествующей версией для MS DOS) пользовательского интерфейса, обширной базой данных помощи и огромного числа действующих примеров применения. Возможно, что недавно появившаяся реализация R4 еще упрочит позиции этой системы.
Почитаемая как лидер среди математических систем Mathematica 2.2.2 по-прежнему заслуживает критики. Примитивность вывода результатов в текстовом режиме и продолжающиеся проблемы с надежностью работы в немалой степени снижают качество этой мощной системы, ориентированной на серьезные аналитические расчеты и имеющей уникальные возможности научной и математической графики. Однако пока эта система критикуется явно недостаточно, чтобы поколебать ее лидерство в области символьной математики. Ясно одно - у системы появился весьма мощный соперник в лице Maple V R3.
MathCAD PLUS 6.0 по-прежнему держит марку системы "для всех", в которой аналитика явно принесена в жертву фантастической простоте общения с системой. Порой эту систему удобно использовать как редактор "живых" математических текстов, причем качество набора формул превосходит получаемое с помощью Microsoft Word 6.0/7.0.
Надо признать, что для большинства неискушенных пользователей избранные возможности символьной математики в MathCAD подобраны очень тщательно и оптимально. Эта система в наибольшей степени подходит на роль инструмента для математических расчетов в вузах и даже школах, особенно в связи с выпуском фирмой SoftLine (Россия) русифицированной версии и возможностью подготовки для нее прекрасно иллюстрированных электронных книг с "живыми" примерами. Жаль лишь, что ее аппаратные "аппетиты" не отличаются скромностью.
Фирме MathSoft стоило бы подумать о том, чтобы ввести в MathCAD полное ядро системы Maple V, предусмотрев возможность вызова любой функции по ее имени, например с помощью уже включенных в систему удобных программных конструкций. Это наверняка превратило бы MathCAD в уникальный математический инструмент, сочетающий лучший пользовательский интерфейс MathCAD с обширными и изысканными математическими возможностями ядра Maple V.
Довольно почетное место среди математических систем занимает MatLAB. Нам пока трудно судить, какие возможности даст эта система при расширении ее новыми пакетами символьных операций. Но одно несомненно - это очень мощная система для численных расчетов, особенно матричных, с прекрасной возможностью чуть ли не безграничного расширения ее пользователем. Выход версии 5.0 этой системы может существенно повысить ее оценку в ближайшем будущем.
Среди описанных систем Derive занимает последнее место. Пожалуй, это закономерный итог для простой системы под DOS с примитивным интерфейсом, ориентированной на несложные расчеты в школах и на начальных курсах вузов. Однако и это место почетно без каких либо кавычек, если учесть, с какими монстрами идет сравнение. Derive идеально подходит для начального изучения основ символьной математики, особенно в тех учебных заведениях, где все еще применяются ПК с 286-ми и 386-ми процессорами. Возможно, давно ожидаемый выход версии этой системы под Windows упрочит ее положение на рынке систем символьной математики.
Таким образом, все рассмотренные системы имеют свои ниши в области решения математических и научно-технических задач. Существующий выбор среди систем означает зрелость их развития и возможность эффективного применения на практике. Весьма актуальным для России был бы выход справочных и учебных книг по таким системам (пока есть только выпущенная в 1996 г. книга по Derive и перевод фирменного описания системы MathCAD PLUS 6.0). Между тем за рубежом имеются десятки руководств по применению каждой из указанных выше систем в образовании, для научно-технических расчетов и т. д.
* Следует отметить, что под Windows 95 система Mathematica работает гораздо стабильнее, чем под предыдущими версиями Windows 3.x. - Прим. ред.
Владимир Дьяконов, Андрей Пеньков
Дьяконов Владимир Павлович - д. т. н., проф., директор Смоленского областного центра новых информационных технологий в образовании. С ним можно связаться по телефону: (08122) 6-77-88 или по E-mail: dyakonov@smcnit.su.
Пеньков Андрей Анатольевич - аспирант кафедры промышленной электроники Смоленского филиала МЭИ.
По скромности своих аппетитов вне конкуренции Derive. Неплохо зарекомендовала себя Maple V R3 - это единственная из новейших систем символьной математики, которая все еще работает на ПК с ОЗУ емкостью всего 4 Мб. Что касается MatLAB 4.2, то она при численных расчетах тянет даже с 4 Мб ОЗУ, но для применения графики требует уже 8 Мб.
Derive - простейшая система компьютерной алгебры, имеющая весьма скромные запросы к аппаратной части и довольно развитые возможности аналитических вычислений. Недостатки системы: примитивный интерфейс и слабая графика. Прекрасно подходит на роль математического помощника школьникам и студентам младших курсов вузов.
MatLAB 4.2 - мощная развиваемая пользователем матричная система для численных расчетов. Прародительница ряда математических систем. Символьные вычисления возможны при использовании расширений этой дорогой системы.
Mathematica 2.2.2 - по-прежнему лидер среди систем символьной математики. Отличается уникальными возможностями математической графики.
Maple V R3 - содержит в ядре символьных операций почти 2800 функций и правил преобразования. Имеет массу примеров применения и превосходную графику. В гонке за лидерство уверенно догоняет систему Mathematica 2.2.2.
MathCAD PLUS 6.0 - система с изумительным пользовательским интерфейсом, но ограниченными возможностями символьных вычислений. Эта система "для всех" позволяет готовить электронные книги.
+----------------+-----------------+--------------------------+
|Система | Тип процессора |Минимальная емкость ОЗУ, |
| | ПК | Мб |
+----------------+-----------------+--------------------------+
|Derive 2.6 | 8086 и выше | 0,64 |
+----------------+-----------------+--------------------------+
|MathCAD +6.0 | 386 и выше | 8 |
+----------------+-----------------+--------------------------+
|Maple V R3 | 386 и выше | 4 |
+----------------+-----------------+--------------------------+
|Mathematica | 386 и выше | 8 |
|2.2.2 | | |
+----------------+-----------------+--------------------------+
|MatLAB 4.2 | 386 и выше | 4 - 8 |
+----------------+-----------------+--------------------------+
Где купить
Систему Derive в России реализует дилер фирмы Soft Warehouse МНИИТЦ "Скан" (119021, Москва, ул. Л. Толстого, д. 22./5). По поводу приобретения других систем следует обращаться в корпорацию SoftLine (121087, Москва, а/я 362 или по E-mail: root@softline.msk.su).